
After a quick look into why filters in convolution layers are so useful, I can understand bigger kernels are needed. But why do we need input shapes? In Conv2d layer, the kernel size and filters have direct influence on the accuracy of the model. If you use small kernel or small filters, your accuracy will be low. Another aspect of the conv2d layer is the input shape. The input shape might contain some zeros or ones, which is what is called as bad input. For example, the input shape of a layer can contain zeros or ones. The zeros or ones will have impact on the performance of the model.
In this post, we will look at the use of convolutional layers in convolutional neural networks (CNN). We will discuss the concepts of filter, kernel size, and shape of the input, and how to use them in Conv2d layer in the context of CNNs. Convolutional layers are capable of extracting various features from an image, such as edges, textures, objects and scenes. The convolutional layer contains a set of filters whose parameters need to be examined. It calculates the scalar product between its filter and a small area of the input image. This could yield a volume of [28x28x10] if we decide to use 10 filters.
What is a filter
The convolution layer computes the convolution operation of the input images using feature extraction filters and analyzes the entire image by viewing it through this filter. The filter is shifted by the width and height of the input, and the dot products between the input and the filter are calculated at each position. The output of the convolution is called the feature map. Each filter is folded with the inputs to calculate an activation map. The output volume of the convolution layer is obtained by summing the activation maps of all depth measurement filters. For example, the following scene image filters for feature extraction and activation map calculation. This filter is sometimes called Windows or Kernel – which all mean the same thing in terms of folding neural networks. We can scan an image with multiple filters to display multiple image features. Each feature map shows the parts of the image that express a particular feature defined by our filter parameters. Each convolutional layer consists of several filters. In practice, this is a number such as 32, 64, 128, 256, 512, etc. This number is equal to the number of channels at the output of the convolution layer.
Set filter
In practice, we do not explicitly define the filters that our convolutional layer will use, but rather define the filter parameters and let the network use the best filters in a learning process. We need to determine how many filters we want to use on each layer. During training, the filter values are optimized by backpropagation, taking into account the loss function.
Core size
Each filter has a certain width and height, but the height and weight of the filters (core) are smaller than the input volume. The filters have the same dimensionality but with smaller constant parameters compared to the input images. For example, to calculate a three-dimensional image [32, 32, 3], an acceptable filter size is f × f × 3, where f = 3, 5, 7, etc. kernel_size: the size of these convolutional filters. In practice, they take values like 1×1, 3×3 or 5×5. They can be written briefly as 1, 3 or 5, because in practice they are usually square.
Input layer
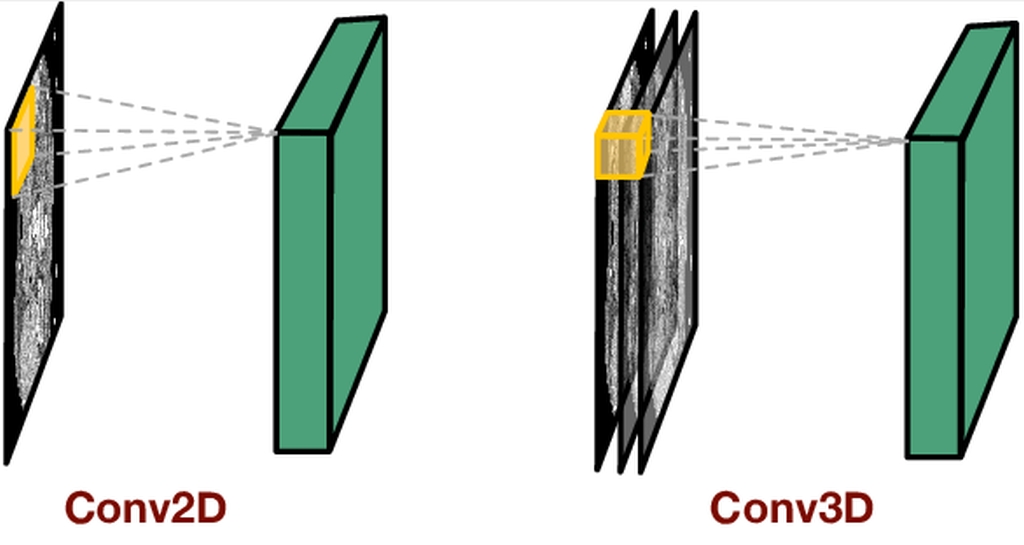
The input layer is conceptually different from the other layers. It stores the raw pixel values of the image. In Keras, the input layer itself is not a layer, but a tensor. This is the initial tensor that sends you to the first hidden layer. This tensor must have the same shape as your training data.
Entry form
The input form is the only thing you need to define, since your template can’t know it. It is based on your training data. All other shapes are automatically calculated according to the units and characteristics of each layer. If you z. B. you have 100 images of dimensions 32x32x3 pixels, your input form would be (100,32,32,3). Then the tensor of your input layer should have this form.This is the first post in a three part series. The first post is about which convolutional neural network architectures we should be using in our deep learning convolutional networks, and it also looks into which filters we should be using for which types of images. In the second part, we look at the kernel size to use in our convolutional layers. The third part of the series will look into the input shape, which is the shape of the output of the convolutional layers.



